剑指Offer面试题:21.从上到下打印二叉树
一、题目:从上到下打印二叉树
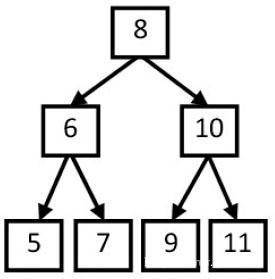
题目:从上往下打印出二叉树的每个结点,同一层的结点按照从左到右的顺序打印。例如输入下图中的二叉树,则依次打印出8、6、10、5、7、9、11。
二叉树节点的定义如下,采用C#语言描述:
public class BinaryTreeNode { public int Data { get; set; } public BinaryTreeNode leftChild { get; set; } public BinaryTreeNode rightChild { get; set; } public BinaryTreeNode(int data) { this.Data = data; } public BinaryTreeNode(int data, BinaryTreeNode left, BinaryTreeNode right) { this.Data = data; this.leftChild = left; this.rightChild = right; } }
二、解题思路
2.1 核心步骤
这道题实质是考查树的层次遍历(广度优先遍历)算法:
每一次打印一个结点的时候,如果该结点有子结点,则把该结点的子结点放到一个队列的末尾。接下来到队列的头部取出最早进入队列的结点,重复前面的打印操作,直至队列中所有的结点都被打印出来为止。
扩展:如何广度优先遍历一个有向图?这同样也可以基于队列实现。树是图的一种特殊退化形式,从上到下按层遍历二叉树,从本质上来说就是广度优先遍历二叉树。
2.2 代码实现
static void PrintFromTopToBottom(BinaryTreeNode root) { if (root == null) { return; } Queue<BinaryTreeNode> queue = new Queue<BinaryTreeNode>(); queue.Enqueue(root); while (queue.Count > 0) { BinaryTreeNode printNode = queue.Dequeue(); Console.Write("{0}\t", printNode.Data); if (printNode.leftChild != null) { queue.Enqueue(printNode.leftChild); } if (printNode.rightChild != null) { queue.Enqueue(printNode.rightChild); } } }
三、单元测试
本次测试封装了几个辅助测试的方法,实现如下:

static void TestPortal(string testName, BinaryTreeNode root) { if (!string.IsNullOrEmpty(testName)) { Console.WriteLine("{0} begins:", testName); } Console.WriteLine("The nodes from top to bottom, from left to right are:"); PrintFromTopToBottom(root); Console.WriteLine("\n"); } static void SetSubTreeNode(BinaryTreeNode root, BinaryTreeNode lChild, BinaryTreeNode rChild) { if (root == null) { return; } root.leftChild = lChild; root.rightChild = rChild; } static void ClearUpTreeNode(BinaryTreeNode root) { if(root != null) { BinaryTreeNode left = root.leftChild; BinaryTreeNode right = root.rightChild; root = null; ClearUpTreeNode(left); ClearUpTreeNode(right); } }
3.1 功能测试
// 10 // / \ // 6 14 // /\ /\ // 4 8 12 16 static void Test1() { BinaryTreeNode node10 = new BinaryTreeNode(10); BinaryTreeNode node6 = new BinaryTreeNode(6); BinaryTreeNode node14 = new BinaryTreeNode(14); BinaryTreeNode node4 = new BinaryTreeNode(4); BinaryTreeNode node8 = new BinaryTreeNode(8); BinaryTreeNode node12 = new BinaryTreeNode(12); BinaryTreeNode node16 = new BinaryTreeNode(16); SetSubTreeNode(node10, node6, node14); SetSubTreeNode(node6, node4, node8); SetSubTreeNode(node14, node12, node16); TestPortal("Test1", node10); ClearUpTreeNode(node10); } // 5 // / // 4 // / // 3 // / // 2 // / // 1 static void Test2() { BinaryTreeNode node5 = new BinaryTreeNode(5); BinaryTreeNode node4 = new BinaryTreeNode(4); BinaryTreeNode node3 = new BinaryTreeNode(3); BinaryTreeNode node2 = new BinaryTreeNode(2); BinaryTreeNode node1 = new BinaryTreeNode(1); node5.leftChild = node4; node4.leftChild = node3; node3.leftChild = node2; node2.leftChild = node1; TestPortal("Test2", node5); ClearUpTreeNode(node5); } // 1 // \ // 2 // \ // 3 // \ // 4 // \ // 5 static void Test3() { BinaryTreeNode node5 = new BinaryTreeNode(5); BinaryTreeNode node4 = new BinaryTreeNode(4); BinaryTreeNode node3 = new BinaryTreeNode(3); BinaryTreeNode node2 = new BinaryTreeNode(2); BinaryTreeNode node1 = new BinaryTreeNode(1); node1.rightChild = node2; node2.rightChild = node3; node3.rightChild = node4; node4.rightChild = node5; TestPortal("Test3", node1); ClearUpTreeNode(node5); } // 树中只有1个结点 static void Test4() { BinaryTreeNode node1 = new BinaryTreeNode(1); TestPortal("Test4", node1); ClearUpTreeNode(node1); } // 树中木有结点 static void Test5() { TestPortal("Test5", null); }
3.2 测试结果
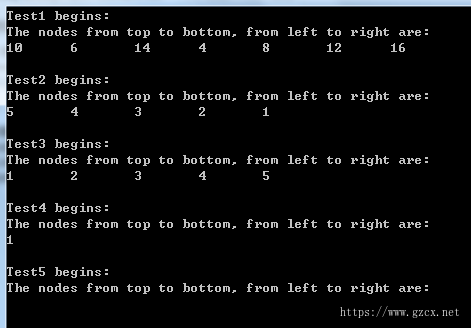
正文到此结束