剑指Offer面试题:33.二叉树的深度
一、题目一:二叉树的深度
1.1 题目说明
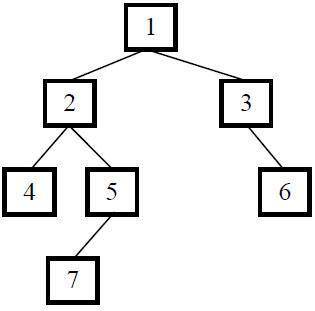
题目一:输入一棵二叉树的根结点,求该树的深度。从根结点到叶结点依次经过的结点(含根、叶结点)形成树的一条路径,最长路径的长度为树的深度。例如下图中的二叉树的深度为4,因为它从根结点到叶结点最长的路径包含4个结点(从根结点1开始,经过结点2和结点5,最终到达叶结点7)。
二叉树的结点定义如下,这里使用C#语言描述:
public class BinaryTreeNode { public int Data { get; set; } public BinaryTreeNode LeftChild { get; set; } public BinaryTreeNode RightChild { get; set; } public BinaryTreeNode(int data) { this.Data = data; } public BinaryTreeNode(int data, BinaryTreeNode left, BinaryTreeNode right) { this.Data = data; this.LeftChild = left; this.RightChild = right; } }
1.2 解题思路
①如果一棵树只有一个结点,它的深度为1。
②如果根结点只有左子树而没有右子树,那么树的深度应该是其左子树的深度加1;同样如果根结点只有右子树而没有左子树,那么树的深度应该是其右子树的深度加1。
③如果既有右子树又有左子树,那该树的深度就是其左、右子树深度的较大值再加1。
比如在上图的二叉树中,根结点为1的树有左右两个子树,其左右子树的根结点分别为结点2和3。根结点为2的左子树的深度为3,而根结点为3的右子树的深度为2,因此根结点为1的树的深度就是4。
public static int GetTreeDepth(BinaryTreeNode root) { if (root == null) { return 0; } int left = GetTreeDepth(root.LeftChild); int right = GetTreeDepth(root.RightChild); return left >= right ? left + 1 : right + 1; }
1.3 单元测试
(1)测试用例
[TestClass] public class TreeDepthTest { private void SetSubTreeNode(BinaryTreeNode root, BinaryTreeNode lChild, BinaryTreeNode rChild) { if (root == null) { return; } root.LeftChild = lChild; root.RightChild = rChild; } private void ClearUpTreeNode(BinaryTreeNode root) { if (root != null) { BinaryTreeNode left = root.LeftChild; BinaryTreeNode right = root.RightChild; root = null; ClearUpTreeNode(left); ClearUpTreeNode(right); } } // 1 // / \ // 2 3 // /\ \ // 4 5 6 // / // 7 [TestMethod] public void GetDepthTest1() { BinaryTreeNode node1 = new BinaryTreeNode(1); BinaryTreeNode node2 = new BinaryTreeNode(2); BinaryTreeNode node3 = new BinaryTreeNode(3); BinaryTreeNode node4 = new BinaryTreeNode(4); BinaryTreeNode node5 = new BinaryTreeNode(5); BinaryTreeNode node6 = new BinaryTreeNode(6); BinaryTreeNode node7 = new BinaryTreeNode(7); SetSubTreeNode(node1, node2, node3); SetSubTreeNode(node2, node4, node5); SetSubTreeNode(node3, null, node6); SetSubTreeNode(node5, node7, null); int actual = TreeDepthHelper.GetTreeDepth(node1); Assert.AreEqual(actual, 4); ClearUpTreeNode(node1); } // 1 // / // 2 // / // 3 // / // 4 // / // 5 [TestMethod] public void GetDepthTest2() { BinaryTreeNode node1 = new BinaryTreeNode(1); BinaryTreeNode node2 = new BinaryTreeNode(2); BinaryTreeNode node3 = new BinaryTreeNode(3); BinaryTreeNode node4 = new BinaryTreeNode(4); BinaryTreeNode node5 = new BinaryTreeNode(5); SetSubTreeNode(node1, node2, null); SetSubTreeNode(node2, node3, null); SetSubTreeNode(node3, node4, null); SetSubTreeNode(node4, node5, null); int actual = TreeDepthHelper.GetTreeDepth(node1); Assert.AreEqual(actual, 5); ClearUpTreeNode(node1); } // 1 // \ // 2 // \ // 3 // \ // 4 // \ // 5 [TestMethod] public void GetDepthTest3() { BinaryTreeNode node1 = new BinaryTreeNode(1); BinaryTreeNode node2 = new BinaryTreeNode(2); BinaryTreeNode node3 = new BinaryTreeNode(3); BinaryTreeNode node4 = new BinaryTreeNode(4); BinaryTreeNode node5 = new BinaryTreeNode(5); SetSubTreeNode(node1, null, node2); SetSubTreeNode(node2, null, node3); SetSubTreeNode(node3, null, node4); SetSubTreeNode(node4, null, node5); int actual = TreeDepthHelper.GetTreeDepth(node1); Assert.AreEqual(actual, 5); ClearUpTreeNode(node1); } // 树中只有1个结点 [TestMethod] public void GetDepthTest4() { BinaryTreeNode node1 = new BinaryTreeNode(1); int actual = TreeDepthHelper.GetTreeDepth(node1); Assert.AreEqual(actual, 1); ClearUpTreeNode(node1); } // 树中没有结点 [TestMethod] public void GetDepthTest5() { int actual = TreeDepthHelper.GetTreeDepth(null); Assert.AreEqual(actual, 0); } }
(2)测试结果
①测试通过情况
②代码覆盖率
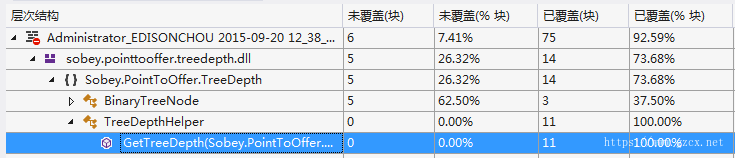
二、题目二:判断二叉树是否是平衡二叉树
2.1 题目说明
题目二:输入一棵二叉树的根结点,判断该树是不是平衡二叉树。如果某二叉树中任意结点的左右子树的深度相差不超过1,那么它就是一棵平衡二叉树。例如,下图中的二叉树就是一棵平衡二叉树。
2.2 解题思路
(1)需要重复遍历节点多次的解法
有了求二叉树的深度的经验之后再解决这个问题,我们很容易就能想到一个思路:在遍历树的每个结点的时候,调用函数TreeDepth得到它的左右子树的深度。如果每个结点的左右子树的深度相差都不超过1,按照定义它就是一棵平衡的二叉树。
public static bool IsBalancedBinaryTree(BinaryTreeNode root) { if (root == null) { return true; } int left = GetTreeDepth(root.LeftChild); int right = GetTreeDepth(root.RightChild); int diff = left - right; if (diff > 1 || diff < -1) { return false; } return IsBalancedBinaryTree(root.LeftChild) && IsBalancedBinaryTree(root.RightChild); }
上面的代码固然简洁,但我们也要注意到由于一个结点会被重复遍历多次,这种思路的时间效率不高。例如在IsBalancedBinaryTree方法中输入上图中的二叉树,我们将首先判断根结点(结点1)是不是平衡的。此时我们往函数TreeDepth输入左子树的根结点(结点2)时,需要遍历结点4、5、7。接下来判断以结点2为根结点的子树是不是平衡树的时候,仍然会遍历结点4、5、7。毫无疑问,重复遍历同一个结点会影响性能。
(2)每个节点只需遍历一次的解法
换个角度来思考,如果我们用后序遍历的方式遍历二叉树的每一个结点,在遍历到一个结点之前我们就已经遍历了它的左右子树。只要在遍历每个结点的时候记录它的深度(某一结点的深度等于它到叶节点的路径的长度),我们就可以一边遍历一边判断每个结点是不是平衡的。
public static bool IsBalancedBinaryTree(BinaryTreeNode root) { int depth = 0; return IsBalancedBinaryTreeCore(root, ref depth); } private static bool IsBalancedBinaryTreeCore(BinaryTreeNode root, ref int depth) { if (root == null) { depth = 0; return true; } int left = 0; int right = 0; if (IsBalancedBinaryTreeCore(root.LeftChild, ref left) && IsBalancedBinaryTreeCore(root.RightChild, ref right)) { int diff = left - right; if (diff >= -1 && diff <= 1) { depth = left >= right ? left + 1 : right + 1; return true; } } return false; }
在上面的代码中,我们用后序遍历的方式遍历整棵二叉树。在遍历某结点的左右子结点之后,我们可以根据它的左右子结点的深度判断它是不是平衡的,并得到当前结点的深度。当最后遍历到树的根结点的时候,也就判断了整棵二叉树是不是平衡二叉树。
2.3 单元测试
此方法的单元测试和第一种方法的一致,这里就不再贴出。需要注意的就是在针对二叉树的测试用例中,需要考虑两种:功能测试(平衡的二叉树,不是平衡的二叉树,二叉树中所有结点都没有左/右子树)。特殊输入测试(二叉树中只有一个结点,二叉树的头结点为NULL指针)。