N皇后

51. N皇后

题目描述

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

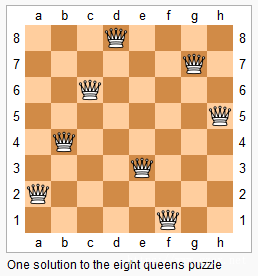
上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例：

``` 输入: 4 输出: [ [".Q..", // 解法 1 "...Q", "Q...", "..Q."],

["..Q.", // 解法 2 "Q...", "...Q", ".Q.."] ] 解释: 4 皇后问题存在两个不同的解法。 ```

问题分析

约束条件为每个棋子所在的行、列、对角线都不能有另一个棋子。

使用一维数组表示一种解法，下标（index）表示行，值（value）表示该行的Q（皇后）在哪一列。
每行只存储一个元素，然后递归到下一行，这样就不用判断行了，只需要判断列和对角线。

Solution1

当result[row] = column时，即row行的棋子在column列。

对于[0, row-1]的任意一行（i 行），若 row 行的棋子和 i 行的棋子在同一列，则有result[i] == column;
若 row 行的棋子和 i 行的棋子在同一对角线，等腰直角三角形两直角边相等，即 row - i == Math.abs(result[i] - column)

布尔类型变量 isValid 的作用是剪枝，减少不必要的递归。 ``` public List> solveNQueens(int n) { // 下标代表行，值代表列。如result[0] = 3 表示第1行的Q在第3列 int[] result = new int[n]; List> resultList = new LinkedList<>(); dfs(resultList, result, 0, n); return resultList; }

void dfs(List> resultList, int[] result, int row, int n) { // 递归终止条件 if (row == n) { List list = new LinkedList<>(); for (int x = 0; x < n; ++x) { StringBuilder sb = new StringBuilder(); for (int y = 0; y < n; ++y) sb.append(result[x] == y ? "Q" : "."); list.add(sb.toString()); } resultList.add(list); return; } for (int column = 0; column < n; ++column) { boolean isValid = true; result[row] = column; / * 逐行往下考察每一行。同列，result[i] == column * 同对角线，row - i == Math.abs(result[i] - column) / for (int i = row - 1; i >= 0; --i) { if (result[i] == column || row - i == Math.abs(result[i] - column)) { isValid = false; break; } } if (isValid) dfs(resultList, result, row + 1, n); } } ```

Solution2

使用LinkedList表示一种解法，下标（index）表示行，值（value）表示该行的Q（皇后）在哪一列。

解法二和解法一的不同在于，相同列以及相同对角线的校验。 将对角线抽象成【一次函数】这个简单的数学模型，根据一次函数的截距是常量这一特性进行校验。

这里，我将右上-左下对角线，简称为“\”对角线；左上-右下对角线简称为“/”对角线。

“/”对角线斜率为1，对应方程为y = x + b，其中b为截距。
对于线上任意一点，均有y - x = b，即row - i = b;
定义一个布尔类型数组anti_diag，将b作为下标，当anti_diag[b] = true时，表示相应对角线上已经放置棋子。
但row - i有可能为负数，负数不能作为数组下标，row - i 的最小值为-n（当row = 0，i = n时），可以加上n作为数组下标，即将row -i + n 作为数组下标。
row - i + n 的最大值为 2n（当row = n，i = 0时），故anti_diag的容量设置为 2n 即可。

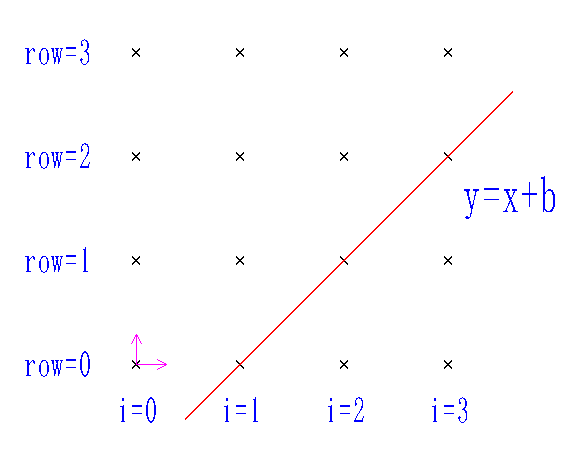
“\”对角线斜率为-1，对应方程为y = -x + b，其中b为截距。
对于线上任意一点，均有y + x = b，即row + i = b;
同理，定义数组main_diag，将b作为下标，当main_diag[row + i] = true时，表示相应对角线上已经放置棋子。

有了两个校验对角线的数组，再来定义一个用于校验列的数组cols，这个太简单啦，不解释。

解法二时间复杂度为O(n!)，在校验相同列和相同对角线时，引入三个布尔类型数组进行判断。相比解法一，少了一层循环，用空间换时间。

``` List> resultList = new LinkedList<>();

public List> solveNQueens(int n) { boolean[] cols = new boolean[n]; boolean[] main_diag = new boolean[2 * n]; boolean[] anti_diag = new boolean[2 * n]; LinkedList result = new LinkedList<>(); dfs(result, 0, cols, main_diag, anti_diag, n); return resultList; }

void dfs(LinkedList result, int row, boolean[] cols, boolean[] main_diag, boolean[] anti_diag, int n) { if (row == n) { List list = new LinkedList<>(); for (int x = 0; x < n; ++x) { StringBuilder sb = new StringBuilder(); for (int y = 0; y < n; ++y) sb.append(result.get(x) == y ? "Q" : "."); list.add(sb.toString()); } resultList.add(list); return; } for (int i = 0; i < n; ++i) { if (cols[i] || main_diag[row + i] || anti_diag[row - i + n]) continue; result.add(i); cols[i] = true; main_diag[row + i] = true; anti_diag[row - i + n] = true; dfs(result, row + 1, cols, main_diag, anti_diag, n); result.removeLast(); cols[i] = false; main_diag[row + i] = false; anti_diag[row - i + n] = false; } } ```